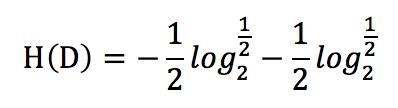适合AI产品经理阅读的算法集合之决策树
正文:
微软小冰推出过一项服务,读心术,回答15个问题【是或否】,即知道你心中所想。这就是决策树的应用,那我们举个例子来简单的讲讲什么是决策树?
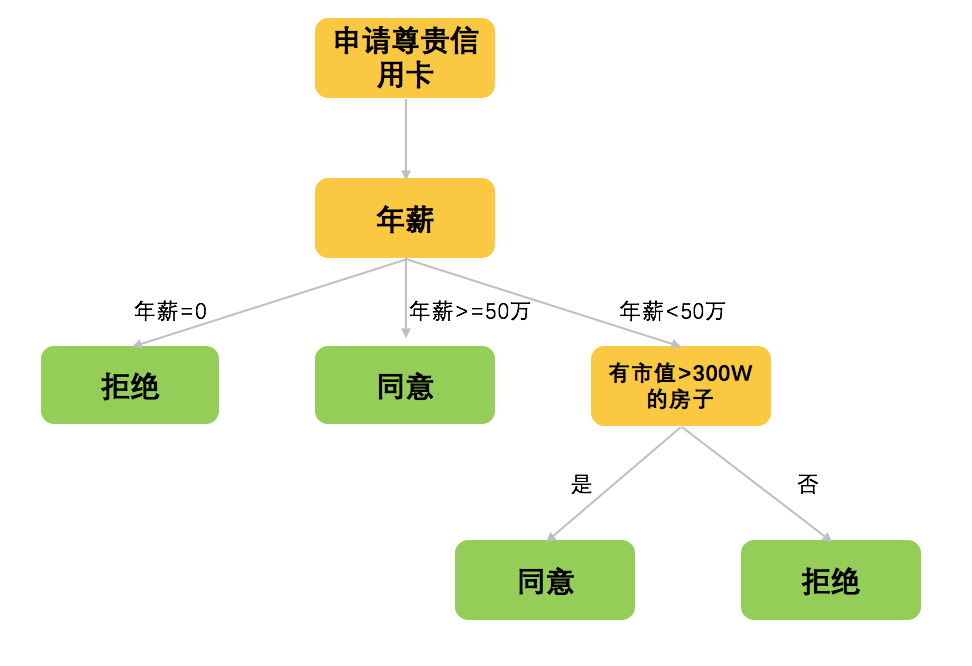
如何来判断某位朋友是否有资质来拥有一张尊贵的信用卡?我们的思路可以如下图所示。
这就是典型的决策树的过程,我们通过机器来判断哪些特征(因素)最优先考虑,哪些特征可以剔除不需要,来构建一个像树一样的决策结构。
让我们考虑下,如果先看房子,再看收入,模型会有怎么样的区别呢?如果我们新增了一个节点—所在城市,模型又会怎样变化呢?
1、 决策树算法步骤

1.1、 标准集
一份标注正确的样本及对应的分类
1.2、 特征建立
建立优秀的特征数据
1.3、 特征选择
如何判断哪个特征应该在树的前面呢?原则上,我们会使用区分度最大的,这里我们就引入了一个信息增益比的概念。不想涉及技术太深的同学,这里可以先不看。理解这个意思就好。本质上,是通过特征的选择,能够让这棵树最简化,所以需要知道特征放在前面好,还是后面好。
我们先来看看信息增益比的公式,由此我们得知道g(D,A)是如何计算的,以及,H(D)如何计算的。
先来看看H(D),经验熵。公式如下【第一个】,我们来举个例子,比如上面的例子中,我们可以发现,2个同意,2个拒绝,那么,这个公式如下【第二个】: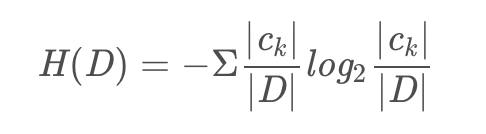
g(D,A)就是信息增益,H(D|A),和H(D)的区别,就是一个是概率,一个是条件概率,在A条件下的D的概率,A是选定的特征,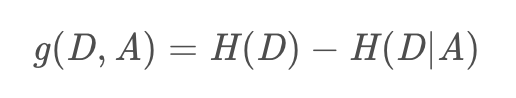
1.4、 构建决策树
构建决策树的方法有三种:C4.5、ID3和CART
ID3
ID3算法是根据决策树各个结点上对应信息增益g(D,A)准则选择特征,递归地构建决策树,由大到小的进行构建。ID3仅仅适用于二分类问题
C4.5
对ID3的改进,使用的是信息增益比gR(D,A)选择特征,递归地构建决策树。
CART
使用 Gini 指数作为选择特征的准则。CART 生成的树必须是二叉树,也就是说,属性值必须是2个。
基尼指数越大,集合不确定性越高,不纯度也越大。这一点和熵类似。那区别是什么呢?
- Gini 指数的计算不需要对数运算,更加高效;
- Gini 指数更偏向于连续属性,熵更偏向于离散属性。
1.4、 修剪决策树
为什么我们需要修剪决策树?
决策树算法很容易过拟合(overfitting),剪枝算法就是用来防止决策树过拟合,提高泛华性能的方法。为什么决策树算法会过于拟合?原因在于在学习时过多的考虑如何提高对训练数据的正确分类,从而构建出过于复杂的决策树,解决方法是考虑决策树的复杂度,对已经生成的树进行简化。
剪枝分为预剪枝与后剪枝。
- 预剪枝是指在决策树的生成过程中,对每个节点在划分前先进行评估,若当前的划分不能带来泛化性能的提升,则停止划分,并将当前节点标记为叶节点。
- 后剪枝是指先从训练集生成一颗完整的决策树,然后自底向上对非叶节点进行考察,若将该节点对应的子树替换为叶节点,能带来泛化性能的提升,则将该子树替换为叶节点。
#适合AI产品经理阅读的算法集合系列。 该系列文章,主旨在于,用非技术性的语言,向大家介绍算法相关的模型和思路,让大家看的懂,听得懂。